The concept of fractions, particularly improper fractions, is not foreign to any individual who has ventured through the realm of mathematics. An improper fraction, as its name implies, is a fraction in which its numerator is greater than or equal to its denominator. In today’s in-depth exploration, we will delve into the intriguing world of improper fractions, particularly examining the number 1 2/7 and its improper fraction equivalent.
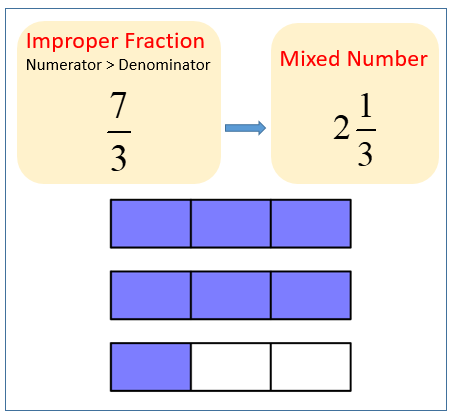
Image: www.onlinemathlearning.com
What is an Improper Fraction?
To comprehend the essence of improper fractions, envision a fraction as a slice of a pizza. A conventional fraction, like 2/5, represents a portion of that pizza, where 2 out of 5 equal slices belong to us. However, in the case of an improper fraction, such as 7/5, we are faced with a scenario where the number of slices we possess (7) surpasses the total number of slices in the pizza (5).
Improper fractions signify quantities greater than one, a notion opposed to proper fractions (e.g., 2/5) that indicate quantities less than one. As such, improper fractions can be expressed as mixed numbers, which elegantly blend the wholes and fractional parts of a quantity. For instance, 1 2/7, the focal point of our study, can be readily converted to a mixed number by ascertaining the integer portion.
Converting 1 2/7 to an Improper Fraction
Transforming 1 2/7 into an improper fraction entails a straightforward procedure that hinges upon the fundamental concept of equivalent fractions. Equivalent fractions represent the same value despite having different numerators and denominators. For example:
1/2 = 2/4 = 3/6 Envision the fraction 1 2/7 as a pizza. The whole number (1) embodies a complete pizza, while the fraction (2/7) represents two slices out of a total of seven. To express this as an improper fraction, we must determine the equivalent fraction that incorporates the whole pizza plus the fractional slices:
1 2/7 = 7/7 + 2/7 = 9/7Hence, we unveil that 1 2/7, when rendered as an improper fraction, translates to 9/7.
Real-World Applications of Improper Fractions
Contrary to what one might initially surmise, improper fractions are far from being mere mathematical abstractions. They play indispensable roles in a surprisingly broad spectrum of real-world applications, such as:
- Cooking: Recipes frequently employ improper fractions to indicate ingredient quantities, enabling adjustments based on the number of individuals being served or the desired serving size.
- Physics: Improper fractions aid in expressing ratios and proportions, which are crucial for calculations involving speed, distance, and other physical quantities.
- Finance: Banks often utilize improper fractions to calculate interest rates, facilitating precise computations of accumulated interest over time.
- Time Measurement:
Improper fractions are instrumental in measuring precise units of time. For instance, the duration of 1 hour and 30 minutes can be expressed as the improper fraction 90/60.

Image: ideaswithknowledge.blogspot.com
1 2 7 As An Improper Fraction
Conclusion
Our journey into the realm of improper fractions, exemplified by the conversion of 1 2/7 to its improper fraction form, 9/7, illuminates their profound significance within the sphere of mathematics and various real-world domains. Whether used in baking a cake, calculating velocity, or measuring time, improper fractions serve as indispensable tools for expressing quantities and performing accurate computations. Their versatility underscores the pervasive power of mathematics in our everyday lives.
