Image: www.youtube.com
In the tapestry of mathematics, arcs and central angles dance hand in hand, forming the framework for unraveling geometric puzzles. Whether you’re a budding mathematician or simply seeking to quench your thirst for knowledge, this comprehensive guide will empower you to conquer the enigma of arcs and central angles. From grasping their fundamental concepts to effortlessly finding their elusive measures, we’ll embark on an illuminating journey together.
An Arc-ing Narrative
An arc, like a graceful crescent moon, adorns the circumference of a circle, characterized by two endpoints that embrace a portion of the circle’s grand expanse. Central to this cosmic dance of geometry lies the central angle, a cardinal point that signals the precise angle subtended at the circle’s enigmatic heart. Together, they paint a symphony of geometric proportions, interconnected and inseparable within the hallowed halls of calculus and beyond.
Central Angles: Radiating Grandeur
Central angles, imbued with the very essence of angles, amplify their influence from the celestial center of a circle. An ethereal expanse of rotation, central angles emanate from the circle’s point of origin, creating a mesmerizing ballet of radial connections.
Finding the Central Angle’s Elusive Measure
Like explorers traversing uncharted seas, our quest culminates in dissecting the secrets of measuring central angles. Immerse yourself in the following nuggets of wisdom that will illuminate your path:
-
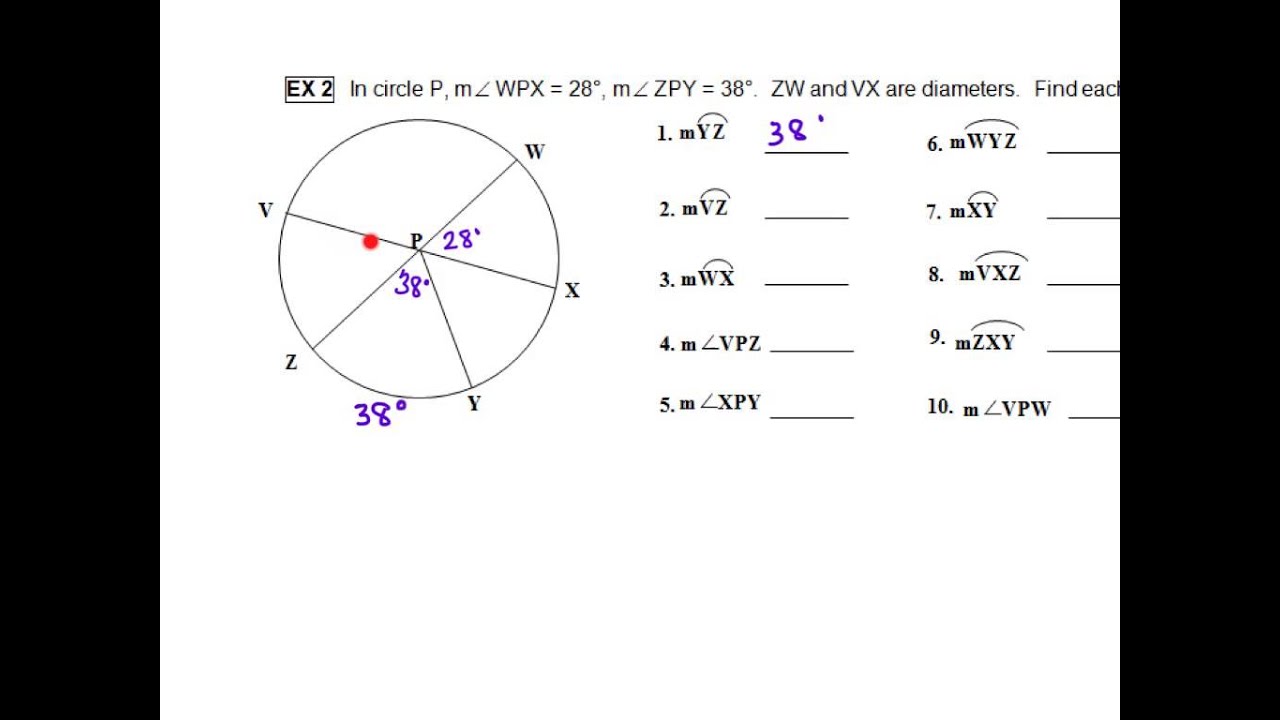
Intercepting Arc: Intercepting arcs, like treasured gems, embody a fraction of the circle’s circumference. Align their radiant curvature with the central angle’s interstellar reach, and you’ve stumbled upon a measure that resounds with the quintessential spirit of the central angle itself.
-
Linear Equation: Embark on an algebraic excursion and introduce an enigmatic variable – let’s call it ‘x’ – that embodies the elusive central angle measure. Employ the potent formula “x = (arc length / radius)” and Eureka! The central angle’s measure, ensnared within the labyrinth of mathematics, reveals its hidden truth.
-
Intersecting Chords: Summon the power of intersecting chords, ethereal entities that dance within the circle’s embrace. Behold their harmonious alignment with the central angle, an elegant symphony of geometry awaiting your discerning eye.
Transforming Arc Length into Angle Measure
When the arc and central angle join forces in a harmonious tango, it’s time to decipher the secrets of intertwining their measurements. Imagine a circle, an embodiment of cosmic perfection, serenely at rest. Now, introduce an arc, a captivating arc, slicing elegantly through the circle’s placid surface. At the heart of this geometric spectacle lies the central angle, a beacon of angular delight. Uncover the enchanting formula that connects them: “Central Angle = (Arc Length / Radius) x (180/π).”
Expert Insights
Renowned mathematicians have dedicated their lives to unraveling the mysteries of arcs and central angles. Allow their profound wisdom to illuminate your path:
-
Albert Einstein, a mind that transcended the boundaries of brilliance, once remarked, “The most beautiful thing we can experience is the mysterious.” Dive into the enigmatic fusion of arcs and central angles, and you’ll discover a tapestry of geometric enchantment.
-
Euclid, the esteemed “Father of Geometry,” implored us to “Let no one who is ignorant of geometry enter here.” As we decipher the secrets of arcs and central angles, let’s embrace this axiom with open hearts and eager minds.
Actionable Guidance
Empower yourself with these invaluable tips for navigating the ethereal realms of arcs and central angles:
-
Visualize the beauty of arcs and central angles gracing the canvas of circles, bringing geometric wonders to life.
-
Dedicate practice sessions to measuring central angles through intercepting arcs, linear equations, and intersecting chords. Each successful endeavor strengthens your geometric arsenal.
-
Immerse yourself in applications where arcs and central angles shine, be it architecture, trigonometry, or engineering. Real-world relevance breathes life into abstract concepts.
Conclusion
Embarking on this geometric voyage, we have traversed the captivating landscapes of arcs and central angles, unraveled their mysteries, and discovered the multifaceted techniques for finding their sought-after measures. Delve into the vast ocean of geometric knowledge that awaits your exploration, where each new discovery will illuminate your path with the brilliance of a thousand stars.
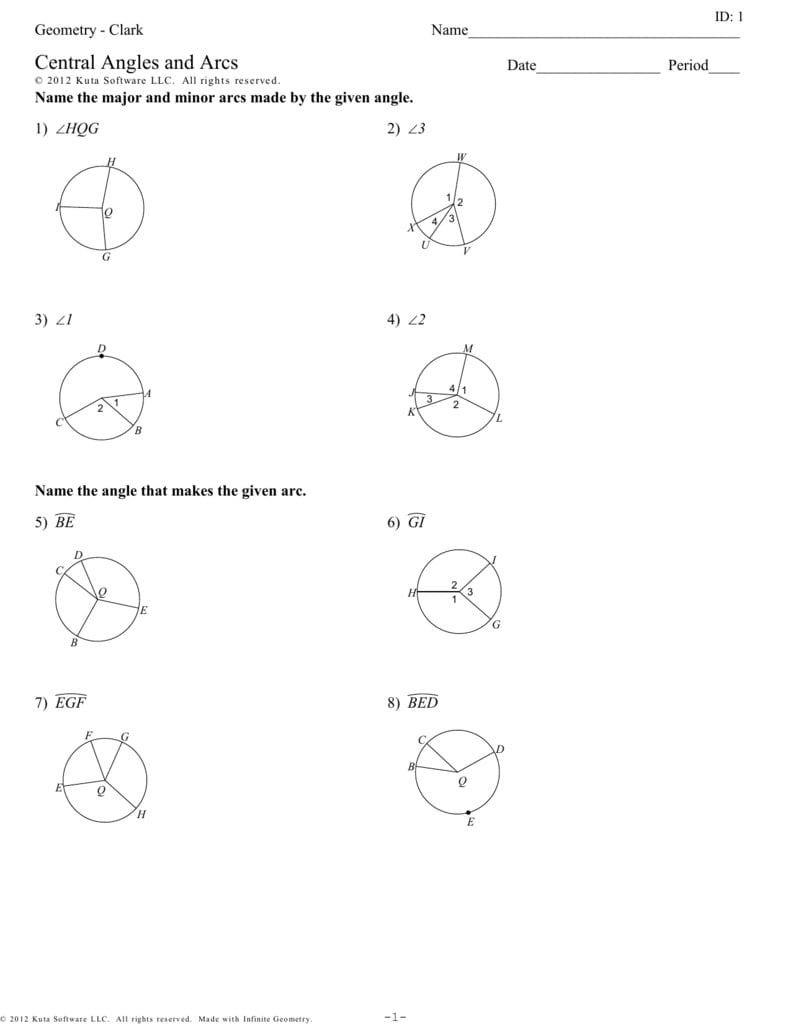
Image: materialmediaverda.z19.web.core.windows.net
Find The Measure Of The Arc Or Central Angle Indicated
