The blue line is a line defined by the equation y = mx + c, whose \(y\)-intercept is \(c\) and \(x\)-intercept is \(-c/m\).
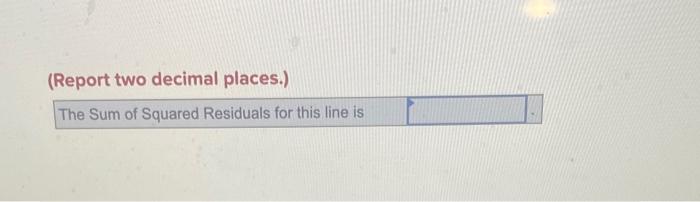
Image: www.chegg.com
Slope of a Blue Line
The steeper the line is, the farther it will stretch. The slope represents changing over time. The rise represents how far \(y\) changes and the run describes how far \(x\) changes. To define the slope with a formula the rise is labelled as: \( (y_2 – y_1) \) and the run as \( (x_2 – x_1) \). Putting them together results in the slope formula \( m = (y_2 – y_1)/(x_2 – x_1) \).
Interesting Facts About \(y = mx + c\)
In this equation, the variable \(m\) represents the slope of the line, while \(c\) denotes the \(y\)-intercept. These two values uniquely characterize any straight line. When \(m\) is positive, the line slants upward from left to right, whereas if \(m\) is negative, it slants downward from left to right.
Applications of \(y = mx + c\)
- Linear Regression: This statistical technique utilizes the equation \(y = mx + c\) to determine the relationship between two variables and predict future values.
- Population Growth: The simple equation helps us calculate the rate of change in a constantly growing population.
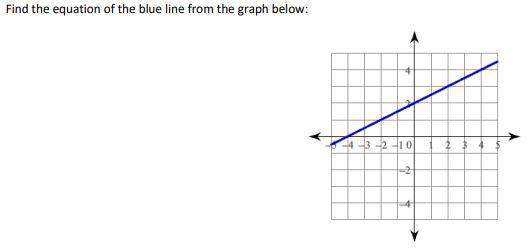
Image: www.chegg.com
Modifications and Extensions
The equation \(y = mx + c\) can be modified and expanded in several ways to represent more complex relationships. For instance, a quadratic equation (y = ax2 + bx + c) models parabolic curves, and a logarithmic equation (y = clog x) captures exponential relationships.
FAQs
How to calculate the slope of a line?
Solution: Find two points on the line and apply the formula \( m = (y_2 – y_1)/(x_2 – x_1)\).
What is an intercept?
Solution: The intercept is the point where the line crosses either the x or y axis. \(x\)-intercept by setting \(y = 0\), and \(y\)-intercept by setting \(x = 0\).
What Is The Equation Of The Blue Line
Conclusion
The equation of a blue line represents the relationship between \(y\) and \(x\), with \(m\) being the slope and \(c\) is the \(y\)-intercept. The blue line is a staple of mathematics, applied profusely in statistics, geometry and economics.
Give me a rating from 1-10. How interesting did you find this article?
1
2
3
4
5
6
7
8
9
10